Rhythmic Variations: a mathematical / music-theoretical exploration (part 1)

 Note: all musical examples in this post can be played back by opening the page here. 

Motivation: Rhythm gets short shrift!
Lately, I've been thinking a lot about rhythm! In a traditional study of music theory, one learns a ton about harmony but very little about rhythm beyond some very basics. Similarly, in studying music history, there's an overemphasis on the harmonic trajectory of Western music, but almost no attention to its rhythmic evolution. And yet often the most salient difference between musical styles is rhythmic. Especially when one considers folk and popular music of the past century, there's a surprising continuity of harmony! Rhythm, however, is another matter.

The point: Math is useful (and fun!) for building on intuition about rhythm and syncopation
This post and the next approach rhythm from a mathematical standpoint, starting with an example of a piece I wrote recently in comparison to one of Bach. In using variations of the main rhythmic theme, I realized most of them were syncopated; this post explains some of the math that backs up that intuitive realization, compares the theme to its obvious Bach counterpart, and motivates further exploration of the topic.

The details:
Here's the new piece:

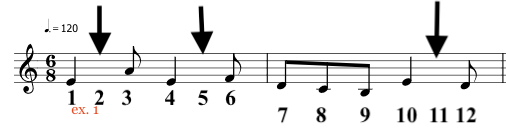
Here's the main theme at the beginning (ex. 1):

Bach aficionados will note the similarity to the Gigue from French Suite no. 4 in E-flat major:

The biggest difference in style between my piece and the Bach gigue is the rhythmic variations that I exploit of the theme. That is, in the Bach, the theme (and indeed most of the piece) rely on the two short rhythms in the first half of measure 1 and first half of measure 2 that you see above in ex. 2.

​There are many purely melodic (that is, intervallic) changes to the theme in the Bach that leave it in tact and recognizable, but essentially no rhythmic changes. In my piece, there's both types of variation. For instance, instead of repeating the first half of the piece (as is typical in Baroque music and happens in the Bach gigue), the second section of my piece starts with the same notes as the main theme over the same duration (two measures), but distributed differently:

As the piece unfolds, several other variations arise that similarly take the same musical idea but in a different rhythms.

The Math:
This raises the question: how many rhythmic variations are there of this melodic idea, keeping the order of the notes, the total duration and (for now) restricting notes to the falling on the beats? The answer will probably surprise you (unless you're already well-versed in the math / combinatorics of the situation): 220. That's a lot!

Here is an explanation (for a more thorough one, scroll down to "combinations" here, or just skip to the next section): there are 9 notes in the idea, and they occur over 12 beats (2 measures with 6 beats each). That means there are going to be 3 "empty" beats without a note beginning on them. Making a choice of a purely rhythmic variation for the 9 notes is equivalent to choosing which 3 beats will be empty. For instance, in example 1 above, the "empty" beats are 2, 5, and 11 (where beat 11 = beat 5 of the second measure). The arrows below point to the empty beats.

In contrast, in example 3 above, beats 3, 5, and 7 are the "empty" beats.

To make a variation, you start with 12 possibilities for the first choice of empty beat. For each of those 12 possibilities, you have 11 possibilities for the second choice of empty beat. Now that you've chosen 2 empty beats, you have 10 possibilities for the third beat. So far, we have 12*11*10 total possibilities, but we've actually double counted a bunch, because the ultimate order of the 3 empty beats doesn't matter. That is, if we choose 2, then 6, then 10, we end up with the same rhythm as if we chose 10, then 2, then 6. So, we divide by 6 because there are 3*2*1 ways to order the 3 empty beats we ended up choosing. We end up with 12*11*10 / (3*2*1) = 220. Mathematicians came up with a shorthand for this type of problem, and would simply call our answer "12 choose 3"

If we had instead chosen where to put our 9 notes instead of our 3 empty beats, we would have ended up with the same answer (12 choose 9 = 12 choose 3), only it would have taken a lot longer to explain!

As one more example, let's say we did choose 2, 6, 10 (or 10, 2, and 6) for our empty beats. What would our melody look like?

Now let's pause for just a second and take note of the fact that there are a lot of possibilities. Way too many to list them all out here, and way too many to insert into a single piece of music (that's of reasonable length). 

The next question is, how many of the rhythmic variations are syncopated vs un-syncopated? Here I'll tell you the answer and follow up with explanation of what it means, why it matters, and how I calculated it in part 2. The answer is: 191 syncopated, 29 un-syncopated. That's a lot more syncopated than not!
​​